LARS notes (Part1) (To page9,2 end)

Abstract:

Useful and less greedy version of traditional forward selection methods.

Main property:

Implement the Lasso, lasso Modification: Calculates all possible Lasso estimates for a given problem.
Different version: Another modification efficiently implements forward stagewise linear regression.
A simple approximation for the degree of freedom of a LARS estimate is available, from which we derive a $C_p$ estimate of prediction error. thisi allws a principled choice among the range of possible LARS estimates.
(Not quite understand the final part of the LARS goals.)

LARS relates: classic model-selection method known as "forward selection" or "forward stepwise regression."

Forward Selection
- Given a collection of possible predictors, select the one largest absolute correlation with the response $y$ , say $x_{j_1}$ , and perform simple linear regression of $y$ on $x_{j_1}$ , than leaves a residual vector which is orthogonal to $x_{j_1}$ . Project the other predictors orthogonally to $x_{j_1}$ nd repeat the selection process. After k steps this results in a set of predictors $x_{j_1},...,x_{j_k}$ that are then used in the usual way to construct a k-parameter linear model.
Forward stagewise
More cautious version of forwad selection-> take thousands tiny steps as it moves toward a final model.
Original motivation for the LARS algorithm.
LARS-Lasso-Stagewise connection is comceptually as well as computationally useful.

Model construction:

Predict response $y$ from covariates $x_1,\cdots,x_n$ .

By location and scale transformations we always assume that the covariates have been standardized to have mean 0 and unit length, and that the response has mean 0.

\sum_{i=1}^n y_i=0\ \ \ \sum_{i=1}^n x_{ij}=0\ \ \ \sum_{i=1}^n x_{ij}^2=1\ \ \ \ \textit{for} \ \ j=1,2,...,m

Regression coefficients : $\widehat { \boldsymbol { \beta } } = \left( \widehat { \beta } _ { 1 } , \widehat { \beta } _ { 2 } , \ldots , \widehat { \beta } _ { m } \right) ^ { \prime }$ gives prediction vector $\hat\mu$

\hat { \boldsymbol { \mu } } = \sum _ { j = 1 } ^ { m } \mathbf { x } _ { j } \hat { \beta } _ { j } = X \hat { \boldsymbol { \beta } } \quad \left[ X _ { n \times m } = \left( \mathbf { x } _ { 1 } , \mathbf { x } _ { 2 } , \ldots , \mathbf { x } _ { m } \right) \right]

Total squared error

S ( \widehat { \boldsymbol { \beta } } ) = \| \mathbf { y } - \widehat { \boldsymbol { \mu } } \| ^ { 2 } = \sum _ { i = 1 } ^ { n } \left( y _ { i } - \widehat { \mu } _ { i } \right) ^ { 2 }

$L_1$ norm for lasso

T ( \widehat { \boldsymbol { \beta } } ) = \sum _ { j = 1 } ^ { m } \left| \widehat { \beta } _ { j } \right|

\textit{Lasso: minimize }\ \ \ S(\hat\beta) \textit{subject to }\ \ \ \ T ( \widehat { \beta } ) \leq t

Quadratic programming techniques can be used to solve (5).though we will present an easier method here, closely related to the “homotopy method” of Osborne, Presnell and Turlach (2000a)."

Forward Stagewise Linear Regression.

Begins with $\hat\mu=0$ ,builds up the regression function in successive small steps.
Let $\hat\mu$ is the current Stagewise estimate, let $\mathbf { c } ( \widehat { \boldsymbol { \mu } } )$ be the vector of current correlations
$\widehat { \mathbf { c } } = \mathbf { c } ( \widehat { \boldsymbol { \mu } } ) = X ^ { \prime } ( \mathbf { y } - \widehat { \boldsymbol { \mu } } )$
$\hat c_j$ is proportional to the correlation between covariate $x_j$ and current residual vector. Next step is taken in the direction of the greatest current correlation,
$\widehat { j } = \operatorname { argmax } \left| \widehat { c } _ { j } \right| \quad \text { and } \quad \widehat { \boldsymbol { \mu } } \rightarrow \widehat { \boldsymbol { \mu } } + \epsilon \cdot \operatorname { sign } \left( \widehat { c } _ { \hat { j } } \right) \cdot \mathbf { x } _ { \hat { j } }$
Need to mentioned here: $\epsilon$ is a "small" constant, "small" is important, otherwise "big" choice like $\epsilon=|\hat c_j|$ leads to the standard forward selection technique. this could be over greedy.

The main point:

LARS is a stylized version of the stagewise procedure that uses a simple mathematical formula to accelerate the computations.

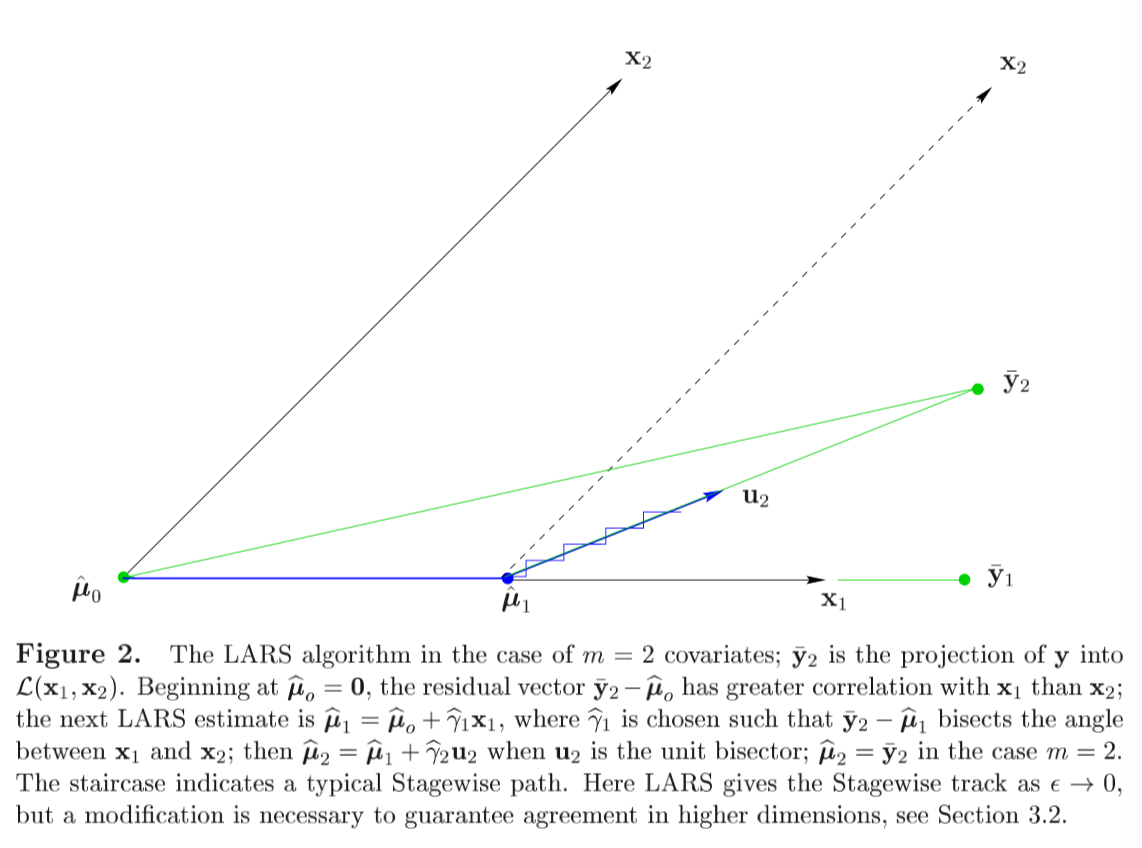
LARSproc

以下是重复论文的无聊描述，参考价值有限，但是因为内容已经高度概括化所以不方便删除，以下是用中文复述一遍主要思想。下午浪费半天一个原因就是因为没注意仔细 $\overline{y_2}$ 是y在 $\mathcal { L } ( X )$ 上的投影，也就是说，如果我们只考虑 $(x_1,x_2)$ ，那么 $\overline y_2$ 就是目标的response. （而且在第一遍看的时候当初理解了这个事实！但是忘了orz）。

$\overline y_2$ 是目标response, 此时， $\overline y_2$ 和 $x_1$ 的correlation比 $x_2$ 大，于是 $\hat\mu_1$ 朝 $x_1$ 更新，然后呢，此时的residual $\overline y_2-\hat\mu_1$ 继续对 $x_1$ 和 $x_2$ 找correlation. 慢慢找，直到如上图 $\hat\mu_1$ 那个点,这时，correlation相等了，那么就停在这里，进行方向切换。而新的方向则是 $x_1$ 和 $x_2$ 的角平分线方向。而LARS的计算过程可以通过一步直接跳到这个需要换方向的点，可以极大的降低计算消耗。（是否能跳过去这里存疑）

Each step adding one covariate to the model, after k steps just k of the $\hat\beta_j$ 's are non-zero. The figure2 showed the m=2 covariates, $X=(x_1,x_2)$ . In this case the current correlation $\widehat { \mathbf { c } } = \mathbf { c } ( \widehat { \boldsymbol { \mu } } ) = X ^ { \prime } ( \mathbf { y } - \widehat { \boldsymbol { \mu } } )$ depend only on the projection $\overline y_2$ of $y$ into the linear space $\mathcal { L } ( X )$ spanned by $x_1$ and $x_2$ .

The algorithm begins at $\hat\mu_0=0$ , Figure 2 has $\overline { \mathbf { y } } _ { 2 } - \widehat { \boldsymbol { \mu } } _ { o }$ making a smaller angle with $x_1$ than $x_2$ . In this case, the new correlation can be expressed as

$\mathbf { c } ( \widehat { \boldsymbol { \mu } } ) = X ^ { \prime } ( \mathbf { y } - \widehat { \boldsymbol { \mu } } ) = X ^ { \prime } \left( \overline { \mathbf { y } } _ { 2 } - \widehat { \boldsymbol { \mu } } \right)$

Then, choose $x_1$ as the direction.

\widehat { \boldsymbol { \mu } } _ { 1 } = \hat { \boldsymbol { \mu } } _ { o } + \widehat { \gamma } _ { 1 } \mathbf { x } _ { 1 }

Stagewise would choose $\hat\gamma_1$ equal to some value $\epsilon$ , than repeat many times, or make $\hat\gamma_1$ larger enough to make $\hat\mu_1$ equal $\overline y_1$ , the projection of y into $\mathcal { L } \left( \mathbf { x } _ { 1 } \right)$ .
LARS uses an intermediate value of $\hat\gamma_1$ , the value that makes $\overline { \mathbf { y } } _ { 2 } - \widehat { \boldsymbol { \mu } }$ , equally correlated with $x_1$ and $x_2$ ; that is, $\overline y_2-\hat\mu_1$ bisects the angle between $x_1$ and $x_2$ , so $c_1(\hat\mu_1)=c_2(\hat\mu_1)$ .
$u_2$ be the unit vector lying along the bisector. The next LARS estimate is
$\widehat { \boldsymbol { \mu } } _ { 2 } = \widehat { \boldsymbol { \mu } } _ { 1 } + \widehat { \gamma } _ { 2 } \mathbf { u } _ { 2 }$
With $\hat\gamma_2$ chosen to make $\hat\mu_2=\overline y_2$ in the case m=2. With $m>2$ covariates , $\hat\gamma_2$ would be smaller, leading to another change of direction.
LARS is motivated by the fact that it is easy to calculate the step size $\hat\gamma_1,\hat\gamma_2,...$ , short-circuiting the small Stagewise steps.

We assume that the covariate vector $x_1,x_2,...,x_m$ are linearly independent.

For $\mathcal { A }$ a subset of the indices $\{1,2,...,m\}$ , define the matix

X _ { \mathcal { A } } = \left( \cdots s _ { j } \mathrm { x } _ { j } \cdots \right) _ { j \in \mathcal { A } }

when the signs $s_j$ equal $\pm 1$ . Let

\mathcal { G } _ { \mathcal { A } } = X _ { \mathcal { A } } ^ { \prime } X _ { \mathcal { A } } \quad \text { and } \quad A _ { \mathcal { A } } = \left( 1 _ { \mathcal { A } } ^ { \prime } \mathcal { G } _ { \mathcal { A } } ^ { - 1 } 1 _ { \mathcal { A } } \right) ^ { - \frac { 1 } { 2 } }

$1 _ { \mathcal { A } }$ being a vector of 1's of length equaling $|\mathcal{A}|$ the size of $\mathcal{A}$ . The

\text { equiangular vector: }u_{A} = X _ { \mathcal { A } } w _ { \mathcal { A } } \quad \text { where } \quad w _ { \mathcal { A } } = A _ { \mathcal { A } } G _ { \mathcal { A } } ^ { - 1 } 1 _ { \mathcal { A } }

is the unit vector making equal angles, less than $90 ^ { \circ }$ , with the column of $X_\mathcal{A}$ ,

X _ { \mathcal { A } } ^ { \prime } \mathbf { u } _ { \mathcal { A } } = A _ { \mathcal { A } } 1 _ { \mathcal { A } } \quad \text { and } \quad \left\| \mathbf { u } _ { \mathcal { A } } \right\| ^ { 2 } = 1

We saw the previous part in a negative direction. First, we look the final part (12), which should be satisfied as the equal angular .

We need find a vector $u_{\mathcal{A}}$ satisfied $X'u=a\mathbf{1}$ , now note that $\mathbb { 1 } = X ^ { \prime } X \left( X ^ { \prime } X \right) ^ { - 1 } \mathbb { 1}$ . That is , we have $X'$ in the left hand side. so $u_\mathcal{A}$ have a candidate $X(X'X)^{-1}\mathbf{1}$ , then what we need to do is just standardize it.

\begin{align} u&=\frac{X(X'X)^{-1}\mathbf{1}}{\sqrt{\mathbf{1}'(X'X)^{-1}X'X(X'X)^{-1}\mathbf{1} }}\\ &=\frac{X(X'X)^{-1}\mathbf{1}}{\sqrt{\mathbf{1}'(X'X)^{-1}\mathbf{1} }}\\ &= \frac{XG^{-1}\mathbf{1}}{\sqrt{\mathbf{1}'G^{-1}\mathbf{1}}}\\ &=X G^{-1}\mathbf{1}\times A\\ &=XA^*G^{-1}\mathbf{1}\\ &=Xw \end{align}

This is how the equal-angular vector is constructed.

So the problem becomes to a nother one, why the form of vector making equal angles?

X _ { \mathcal { A } } ^ { \prime } \mathbf { u } _ { \mathcal { A } } = A _ { \mathcal { A } } 1 _ { \mathcal { A } } \quad

That is, what is this formula mean?

Equal angular is equals to which angular????

That is, the $cos(\theta)$ between any subset $x_{i_\mathcal{A}}$ and $cos<u,x_{i_{\mathcal{A}}}>$ = $\frac{x_{i_{\mathcal{A}}}' u_{\mathcal{A}}}{||x_{i_{\mathcal{A}}}' u_{\mathcal{A}}||}$ . In this case,

$X _ { \mathcal { A } } ^ { \prime } \mathbf { u } _ { \mathcal { A } }$ is the vector about $x_{i_{\mathcal{A}}}' u_{\mathcal{A}}$ , then if the angular is equal, cos also should equal. However, $X'_{\mathcal{A}}$ projection to the direction in $u_{\mathcal{A}}$ , then right hand side is the length of projection times 1. ( $A_{\mathcal{A}}$ is a value rather a matrix.)

The describtion upon is so confusing!!!! need more clear idea about it!!!!

Then is the "fullly" describe about the LARS.

Start with $\hat\mu_0=0$ and build up $\hat\mu$ by steps.
Suppose current estimate is $\hat\mu_{\mathcal{A}}$ ，that $\hat c=X'(y-\hat\mu_{\mathcal{A}})$ , is the current correlations. $\mathcal{A}$ is active set which indices corresponding covariates with the greatest absolute current correlations
$\widehat { C } = \max _ { i } \{ | \widehat { c } _ { j } | \} \quad \text { and } \quad \mathcal { A } = \left\{ j : \left| \hat { c } _ { j } \right| = \widehat { C } \right\}$
Letting
$s _ { j } = \operatorname { sign } \left\{ \widehat { c } _ { j } \right\} \quad \text { for } \quad j \in \mathcal { A }$
we compute $X _ { \mathcal { A } } , A _ { \mathcal { A } }$ and $u_{\mathcal{A}}$ we showed previous, the equal angle trisector and the inner product vector.
$\mathbf { a } \equiv X ^ { \prime } \mathbf { u } _ { \mathcal { A } }$

Then the next step of the LARS algorithm updates $\hat\mu_{\mathcal{A}}$ , say to

\widehat { \boldsymbol { \mu } } _ { \mathcal { A } _ { + } } = \widehat { \boldsymbol { \mu } } _ { \mathcal { A } } + \widehat { \gamma } \mathbf { u } _ { \mathcal { A } }

where

\widehat { \gamma } = \min _ { j \in \mathcal { A } ^ { c } } \left\{ \frac { \widehat { C } - \widehat { c } _ { j } } { A _ { \mathcal { A } } - a _ { j } } , \frac { \widehat { C } + \widehat { c } _ { j } } { A _ { \mathcal { A } } + a _ { j } } \right\}

还是老样子从 $\hat\mu_0=0$ 开始，所以还是两件事，计算当前的correlation $\hat c=X'(y-\hat\mu_{\mathcal{A}})$ . 其中 $\mathcal{A}$ 是一个indices set包括了每一步最大相关系数。这里有点奇怪。特别是 $\hat C$ 的定义形式。

Emmmm，是不是可以这么解释，因为开始转向的时候， $c_1=c_2$ 所以此时往 $u_2$ 的方向走并不会影响 $c_1$ 和 $c_2$ 但是会影响 $c_3$ 。所以等走走走, $c_3$ 又会减小减小。好像不太对，residual的变化。。。。如果按figure2的话，residual对 $x_1$ 的角度一直在增大，角度增大导致correlation会减小，因为 $x_1$ 的 $\gamma$ 在增大， $x_1$ 方向的解释越来越多，而同时，对 $x_2$ 的角度一直在减小,也就是cos在增大，correlation在增大，一减一增两个过程直到这两个correlation相等

然后回到这个过程，也就是在找了一段时间之后，有记录: $\mathcal{A}$ 。注意correlation的定义式： $\hat c=X'(y-\hat\mu_{\mathcal{A}})$ $X$ 是 $n\times p$ ， $p\times n\times n\times1=p\times 1$ ， $\hat c$ 是此时的模型的已建模部分 $\hat\mu_{\mathcal{A}}$ 的residual关于 X的 correlation。

按角平分线的思路,这时候在第 $i$ 维的变化是主要的， $i-1$ 维上应该都是角平分线所以是一致的？

但是 $\mathcal{A}$ 这样定义感觉很奇怪啊。 $\mathcal{A}$ 里面只包含了correlation是最大的那几个，也就是说一直走一直走，走到有新的correlation能加进来，那再改变方向，重新计算 $u_{\mathcal{A}}$ ，否则就一直按这个方向走。比如说回到figure2的图例，在一开始，最大的correlation只有 $x_1$ 这个方向，走一小步， $x_2$ 方向的correlation还是小于 $x_1$ ，所以 $\mathcal{A}$ 还是只有{1}。直到residual 的correlation到 $x_1$ 和 $x_2$ 一致，那么就有了两个同时达到max的correlation，那就得重新计算 $u_\mathcal{A}$ .

那这么理解就没问题了，于是下一步是通过这些东西计算步长.

Back to paper understanding mode

Define:

\boldsymbol { \mu } ( \gamma ) = \widehat { \boldsymbol { \mu } } _ { \mathcal { A } } + \gamma \mathbf { u } _ { \mathcal { A } }

for $\gamma>0$ , so that the current correlation

c_j(\gamma)=x'_j(y-\mu(\gamma))=\hat c_j -\gamma \alpha_j.

for $j\in \mathcal{A}$ , around the equation (20), the definition of correlation, max correlation, direction , yield

\left| c _ { j } ( \gamma ) \right| = \widehat { C } - \gamma A _ { \mathcal { A } }

也就是当前的j的correlation，是最大correlation减去步长乘以和投影向量的长度有关的一个玩意( $A_\mathcal A$ )。注意，这里 $j\in \mathcal{A}$ 。也就和之前描述的，因为走的是角平分线，所以这帮已经active的variable同进退。

然后下一步该考虑的就是不在 $\mathcal{A}$ 里的j。

For $j\in \mathcal{A}^c$ , the two formula upon shows that $c_j(\gamma)$ equals the maximal value at $\gamma=（\hat C-\hat c_j)/(A_\mathcal{A}-a_j)$ . Likewise $-c_j(\gamma)$ , the current correlation for the reversed covariate $-x_j$ , achieves maximality at $（\hat C+\hat c_j)/(A_\mathcal{A}+a_j)$ .

Therefore $\gamma$ in (24), is the smallest positive value of $\gamma$ such that some new index $\hat j$ joins the active set; $\hat j$ is the smallest positive value of $\gamma$ such that some new index $\hat j$ joins the active set; $\hat j$ is the minimizing index in (24) , the foot length of every j in $\mathcal A^c$ . the new active set is $\mathcal { A } \cup \{ \widehat { j } \}$ , the new maximum absolute correlation is $\widehat { C } _ { + } = \widehat { C } - \hat { \gamma } A _ { A }$ .

The figure 10 shows the LARS in diabetes data. 10 iterations for procedure from start to end. The join order or LARS is same as Lasso. However, tracks of $\hat\beta_j$ are nearly but not exactly as either the LASSO or Stagewise tracks.

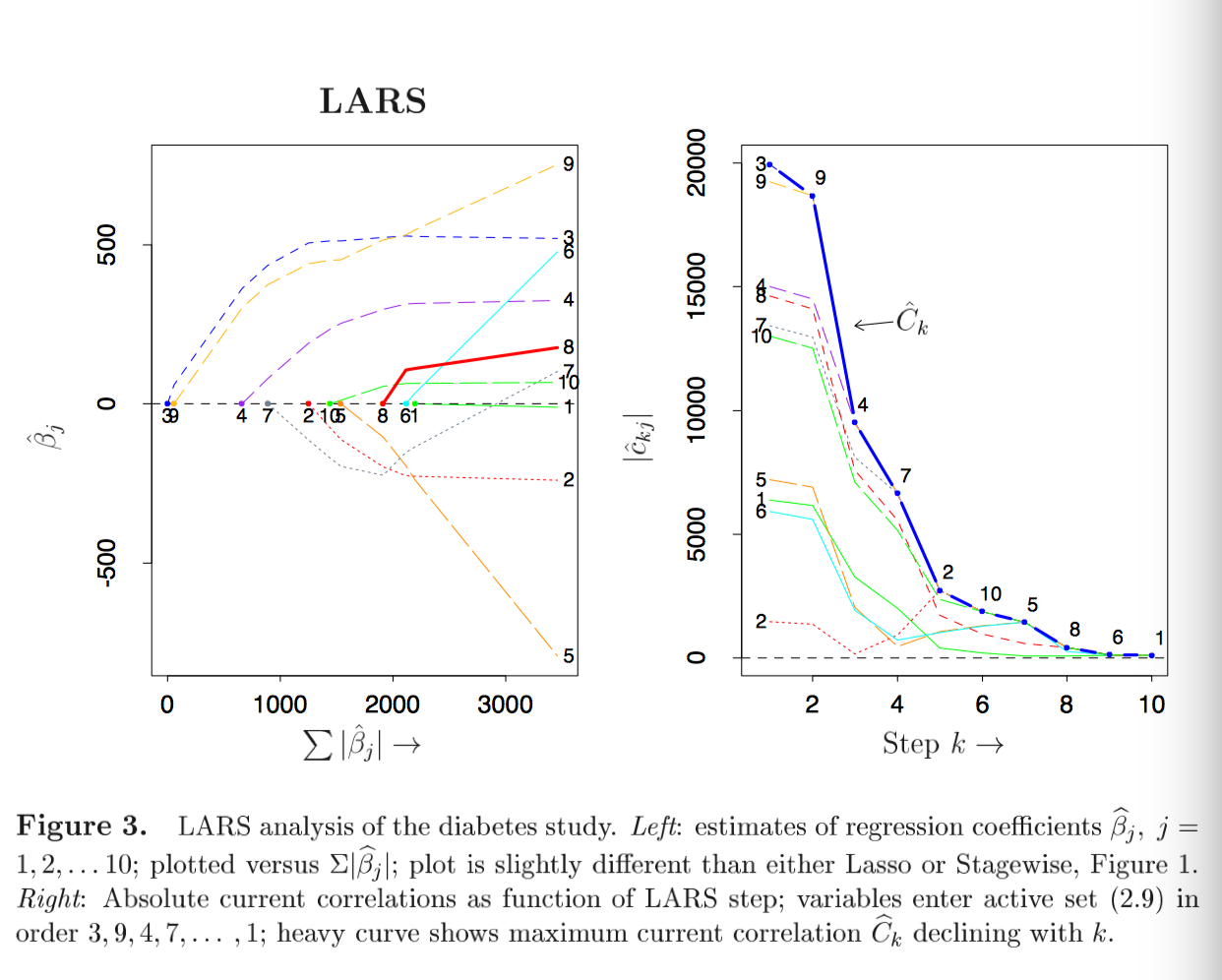
LARSFig3

The right panel shows the absolute current correlation goes done with the LARS step k.

\widehat { C } _ { k } = \max \left\{ \left| \widehat { c } _ { k j } \right| \right\} = \widehat { C } _ { k - 1 } - \widehat { \gamma } _ { k - 1 } A _ { k - 1 }

Declines with k.

Relation between LARS and OLS.

Suppose LARS has just completed step k-1, giving $\hat\mu_{k-1}$ and is embarking upon step k.The active set $\mathcal{A}_k$ will have k members, giving $X _ { k } , \mathcal { G } _ { k } , A _ { k }$ and $u_k$ . Similarly, let $\overline y_k$ indicate the projection of y into $\mathcal { L } \left( X _ { k } \right)$ , which, since $\widehat { \boldsymbol { \mu } } _ { k - 1 } \in \mathcal { L } \left( X _ { k - 1 } \right)$ , is

\overline { \mathbf { y } } _ { k } = \widehat { \boldsymbol { \mu } } _ { k - 1 } + X _ { k } \mathcal { G } _ { k } ^ { - 1 } X _ { k } ^ { \prime } \left( \mathbf { y } - \widehat { \boldsymbol { \mu } } _ { k - 1 } \right) = \widehat { \boldsymbol { \mu } } _ { k - 1 } + \frac { \hat { C } _ { k } } { A _ { k } } \mathbf { u } _ { k }

因为等角性质和Ak里面的东西在correlation上同进退，所以有

X _ { k } ^ { \prime } \left( \mathbf { y } - \widehat { \boldsymbol { \mu } } _ { k - 1 } \right) = \widehat { C } _ { k } 1 _ { \mathcal { A } }

Since $u_k$ is a unit vector, (29) ， $\overline y_k$ 则有 $\overline { \mathbf { y } } _ { k } - \widehat { \boldsymbol { \mu } } _ { k - 1 }$ 有长度

\overline { \gamma } _ { k } \equiv \frac { \widehat { C } _ { k } } { A _ { k } }

和update的那个公式进行比较，则LARS的估计 $\hat\mu_k$ 在 $\hat\mu_{k-1}$ 到 $\overline y_k$ 的延长线上.

\widehat { \boldsymbol { \mu } } _ { k } - \widehat { \boldsymbol { \mu } } _ { k - 1 } = \frac { \hat { \gamma } _ { k } } { \overline { \gamma } _ { k } } \left( \overline { \mathbf { y } } _ { k } - \widehat { \boldsymbol { \mu } } _ { k - 1 } \right)

可以发现一个问题, $\hat\gamma_k$ 总是比 $\overline \gamma_k$ 小，所以 LARS estimates always approaching but never reaching the OLS estimates $\overline y_k$ .

有一个情况例外，如果LARS包含了所有的covariates，然后。。。。反正就和OLS等了。

因为一步到位的性质，LARS算起来特别快。

以上的计算都没有好好看，但是大概意思结论和过程都不复杂所以先放着吧。如果有用再拿起来看。

因为typero打了那么多字好卡，所以暂时把文本分割。

LARS notes (Part1) (To page9,2 end)

Forward Stagewise Linear Regression.

We assume that the covariate vector x_1,x_2,...,x_m are linearly independent.

So the problem becomes to a nother one, why the form of vector making equal angles?

Relation between LARS and OLS.

We assume that the covariate vector $x_1,x_2,...,x_m$ are linearly independent.